 Timings for circuit compression algorithms for XY and TFXY Hamiltonians
Timings for circuit compression algorithms for XY and TFXY Hamiltonians
Abstract
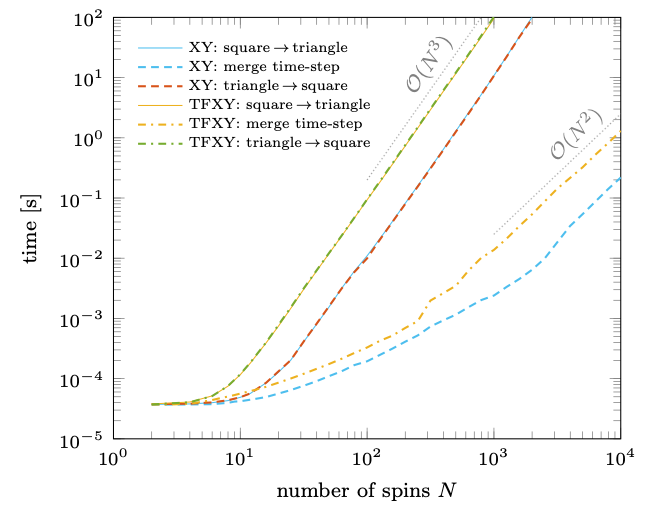
Quantum computing is a promising technology that harnesses the peculiarities of quantum mechanics to deliver computational speedups for some problems that are intractable to solve on a classical computer. Current generation noisy intermediate-scale quantum (NISQ) computers are severely limited in terms of chip size and error rates. Shallow quantum circuits with uncomplicated topologies are essential for successful applications in the NISQ era. Based on matrix analysis, we show that Hamiltonian simulation of certain spin models known as free fermions can be performed in a quantum circuit with a depth that is independent of simulation time and that grows linearly in the number of spins. Our analysis shows how to efficiently and accurately compress these circuits with a numerical algorithm that scales cubically in the number of spins. Numerical experiments show that our circuit synthesis algorithm easily scales up to $O(10^3)$ spins. The resulting quantum circuits have a simple nearest-neighbor topology, which makes them ideally suited for NISQ devices.