Algebraic Compression of Free Fermionic Quantum Circuits: Particle Creation, Arbitrary Lattices and Controlled Evolution
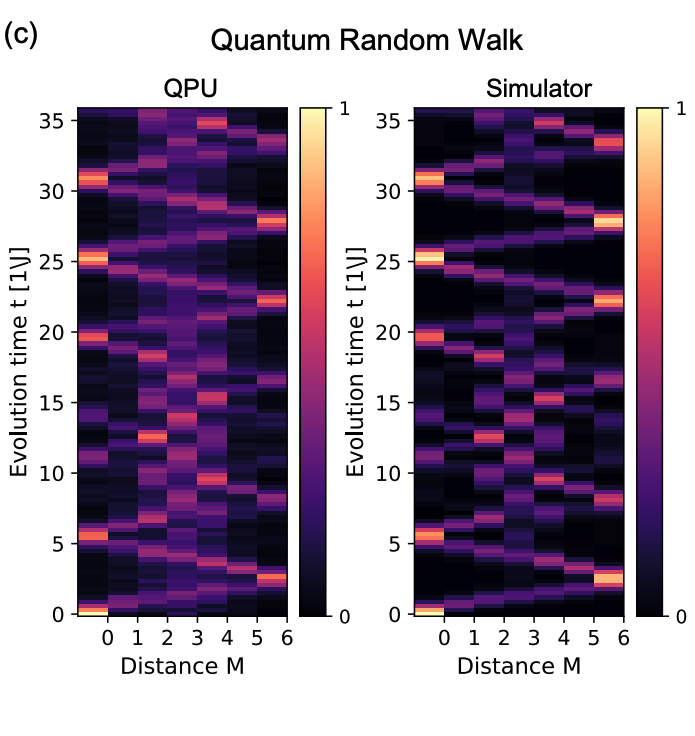 QPU versus simulator results of a fermion undergoing ballistic transport on a 4 x 4 lattice.
QPU versus simulator results of a fermion undergoing ballistic transport on a 4 x 4 lattice.
Abstract
Recently we developed a local and constructive algorithm based on Lie algebraic methods for compressing Trotterized evolution under Hamiltonians that can be mapped to free fermions. The compression algorithm yields a circuit which scales linearly in the number of qubits, is fixed depth for for arbitrarily long evolution times and is applicable to time dependent Hamiltonians, although is limited to simple nearest-neighbor spin interactions and fermionic hopping. In this work, we extend the algorithm to compress circuits simulating evolution with long-range spin interactions and fermionic hopping, thereby enabling embedding of arbitrary lattices onto a chain of qubits. Moreover, we show that controlled time evolution, as well as fermion creation and annihilation operators can also be compressed. We demonstrate our results by adiabatically preparing the ground state for a half-filled fermionic chain, and simulating a 4×4 tight binding model on ibmq_washington. With these new developments, our results enable the simulation of a wider range of models of interest and the efficient compression of subcircuits.