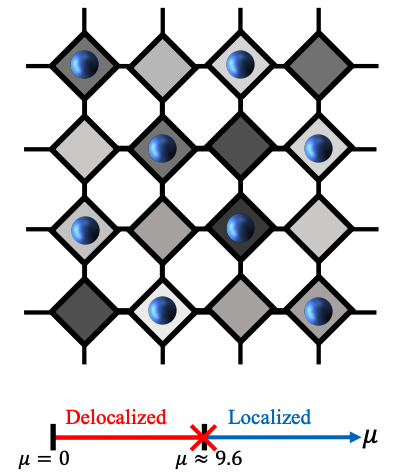
 Simulated 2D model with phase diagram with respect to disorder strength
Simulated 2D model with phase diagram with respect to disorder strength
Abstract
Quantum computers hold the potential to unlock new discoveries in complex quantum systems by enabling the simulation of physical systems that have heretofore been impossible to implement on classical computers due to intractability. A system of particular interest is that of dirty bosons, whose physics highlights the intriguing interplay of disorder and interactions in quantum systems, playing a central role in describing, for instance, ultracold gases in a random potential, doped quantum magnets, and amorphous superconductors. Here, we demonstrate how quantum computers can be used to elucidate the physics of dirty bosons in one and two dimensions. Specifically, we explore the disorder-induced delocalized-to-localized transition using adiabatic state preparation. In one dimension, the quantum circuits can be compressed to small enough depths for execution on currently available quantum computers. In two dimensions, the compression scheme is no longer applicable, thereby requiring the use of large-scale classical state vector simulations to emulate quantum computer performance. In addition, simulating interacting bosons via emulation of a noisy quantum computer allowed us to study the effect of quantum hardware noise on the physical properties of the simulated system. Our results suggest that scaling laws control how noise modifies observables versus its strength, the circuit depth, and the number of qubits. Moreover, we observe that noise impacts the delocalized and localized phases differently. A better understanding of how noise alters the observed properties of the simulated system is essential for leveraging near-term quantum devices for simulation of dirty bosons, and indeed for condensed matter systems in general.