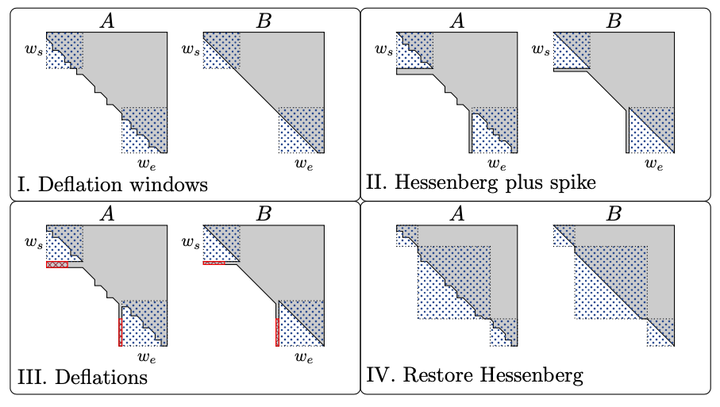
 Aggressive early deflation on block Hessenberg pencils
Aggressive early deflation on block Hessenberg pencils
Abstract
The rational QZ method generalizes the QZ method by implicitly supporting rational subspace iteration. In this paper we extend the rational QZ method by introducing shifts and poles of higher multiplicity in the Hessenberg pencil, which is a pencil consisting of two Hessenberg matrices. The result is a multishift, multipole iteration on block Hessenberg pencils which allows one to stick to real arithmetic for a real input pencil. In combination with optimally packed shifts and aggressive early deflation as an advanced deflation technique we obtain an efficient method for the dense generalized eigenvalue problem. In the numerical experiments we compare the results with state-of-the-art routines for the generalized eigenvalue problem and show that we are competitive in terms of speed and accuracy.