 Middle deflations in a rational QZ algorithm
Middle deflations in a rational QZ algorithm
Abstract
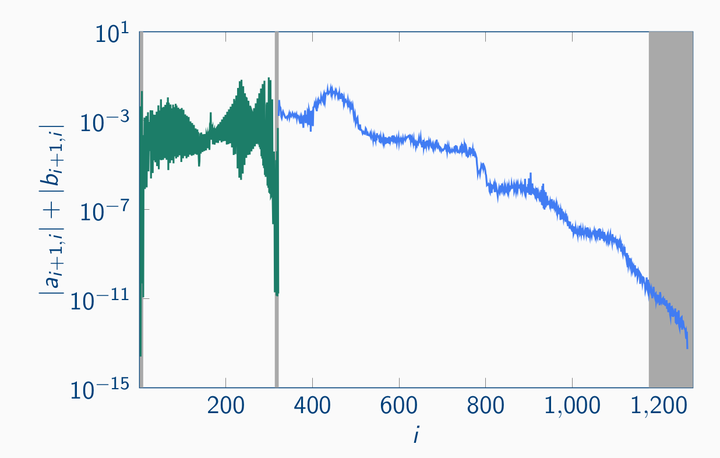
We propose a rational QZ method for the solution of the dense, unsymmetric generalized eigenvalue problem. This generalization of the classical QZ method operates implicitly on a Hessenberg, Hessenberg pencil instead of on a Hessenberg, triangular pencil. Whereas the QZ method performs nested subspace iteration driven by a polynomial, the rational QZ method allows for nested subspace iteration driven by a rational function; this creates the additional freedom of selecting poles. In this article we study Hessenberg, Hessenberg pencils, link them to rational Krylov subspaces, propose a direct reduction method to such a pencil, and introduce the implicit rational QZ step. The link with rational Krylov subspaces allows us to prove essential uniqueness (implicit Q theorem) of the rational QZ iterates as well as convergence of the proposed method. In the proofs, we operate directly on the pencil instead of rephrasing it all in terms of a single matrix. Numerical experiments are included to illustrate competitiveness in terms of speed and accuracy with the classical approach. Two other types of experiments exemplify new possibilities. First we illustrate that good pole selection can be used to deflate the original problem during the reduction phase, and second we use the rational QZ method to implicitly filter a rational Krylov subspace in an iterative method.