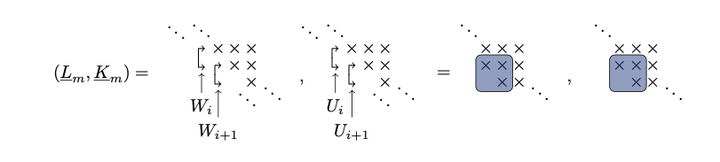 Pole swapping via core transformations
Pole swapping via core transformations
Abstract
The rational Krylov method is a powerful tool for computing a selected subset of eigenvalues in large-scale eigenvalue problems. In this paper we study a method to implicitly apply a filter in a rational Krylov iteration by directly acting on a QR factorized representation of the Hessenberg pair from the rational Krylov method. This filter is used to restart the iteration, which is generally required to limit the orthogonalization and storage costs. The contribution in this paper is three- fold. We reformulate existing procedures in terms of operations on core transformations. This has the advantage of improved convergence monitoring. Secondly, we demonstrate that the extended QZ method is a special case of this more general method. Finally, numerical experiments show the validity and the increased accuracy of the new approach compared with existing methods.