 Ictal EEG data and its tensor decomposition
Ictal EEG data and its tensor decomposition
Abstract
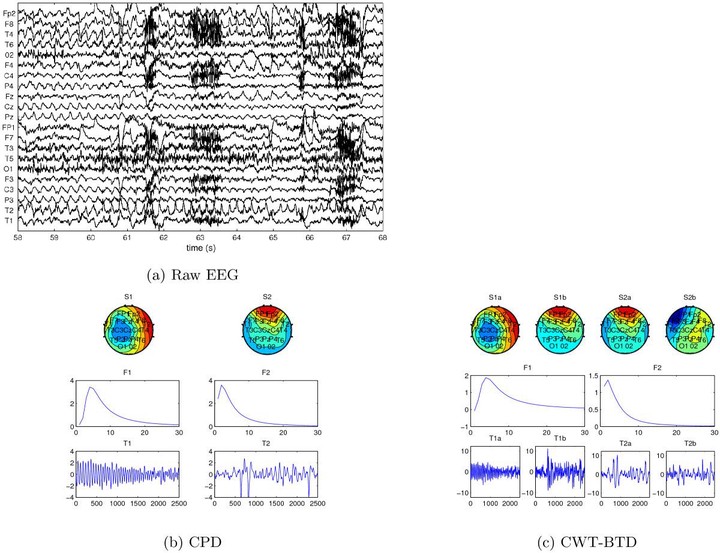
Recordings of neural activity, such as EEG, are an inherent mixture of different ongoing brain processes as well as artefacts and are typically characterised by low signal-to-noise ratio. Moreover, EEG datasets are often inherently multidimensional, comprising information in time, along different channels, subjects, trials, etc. Additional information may be conveyed by expanding the signal into even more dimensions, e.g. incorporating spectral features applying wavelet transform. The underlying sources might show differences in each of these modes. Therefore, tensor-based blind source separation techniques which can extract the sources of interest from such multiway arrays, simultaneously exploiting the signal characteristics in all dimensions, have gained increasing interest. Canonical polyadic decomposition (CPD) has been successfully used to extract epileptic seizure activity from wavelet-transformed EEG data (Bioinformatics 23(13):i10–i18, 2007; NeuroImage 37:844–854, 2007), where each source is described by a rank-1 tensor, i.e. by the combination of one particular temporal, spectral and spatial signature. However, in certain scenarios, where the seizure pattern is nonstationary, such a trilinear signal model is insufficient. Here, we present the application of a recently introduced technique, called block term decomposition (BTD) to separate EEG tensors into rank-$(L_r ,L_r ,1)$ terms, allowing to model more variability in the data than what would be possible with CPD. In a simulation study, we investigate the robustness of BTD against noise and different choices of model parameters. Furthermore, we show various real EEG recordings where BTD outperforms CPD in capturing complex seizure characteristics.